Kontigenstabell

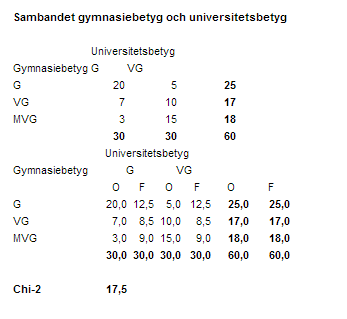
En kontigenstabell är en metod för att testa sambandet mellan två kvalitativa variabler på datanivån nominaldata eller ordinaldata. En kontigenstabell hypotestestas med hjälp av Chi-2 fördelningen som kan användas för alla datanivåer utan att populationerna behöver vara normalfördelade. Förväntade frekvenser i en kontigenstabell beräknas enligt följande:

Förväntade frekvenser:
Radtotal*Kolumntotal/Tabelltotal

Hypotestestning av kontigenstabell
1. Ställ upp nollhypotes och alternativ hypotes
En nollhypotes ställs upp med syftet att den skall testas. En nollhypotes betecknas med H0, där H står för hypotes och 0 för ingen skillnad. En nollhypotes innebär att en populationsparameter inte skiljer sig från det uttalade värdet. En nollhypotes kan antingen förkastas eller inte förkastas, en nollhypotes förkastas endast om vi kan visa att den är falsk. Den alternativa hypotesen är den hypotes som accepteras om vi förkastar nollhypotesen och därmed kan bevisa att nollhypotesen är falsk.

H₀: Det finns inget samband mellan gymnasiebetyg och universitetsbetyg
H₁: Det finns ett samband mellan gymnasiebetyg och universitetsbetyg

2. Välj signifikansnivå
Signifikansnivå är sannolikheten för att förkasta nollhypotesen när den är sann. Det går att välja vilken signifikansnivå som helst mellan 0 och 1, det vanligaste är att använda 0,05 (5%), 0,01 (1%) eller 0,1 (10%). Signifikansnivån måste bestämmas innan en beslutsregel skapas. När man genomför hypotestestning kan man råka ut för två typer av fel, Typ I fel och Typ II fel. Typ I fel innebär att vi förkastar nollhypotesen när den är sann. Typ II fel innebär att vi accepterar nollhypotesen när den är falsk.

3. Beräkna testestimat
Testestimat är ett värde som har bestämts från urvalsinformation och som används för att bestämma huruvida vi skall förkasta nollhypotesen eller inte. Det finns många olika testestimat, Z, t, F och X^2.

X² = ∑((f₀-f_e)^2/f_e)

där:
X² = Chi-2 värdet
f₀ = Observerad frekvens i en cell
f_e = Förväntad frekvens i en cell
∑ = Summa
k = Antalet celler



4. Formulera beslutsregeln
Beslutsregeln är en regel som stipulerar när nollhypotesen skall förkastas och när nollhypotesen inte skall förkastas. I beslutsregeln finns ett kritiskt värde. Ett kritiskt värde är ett X²-värde som har fastställts utifrån signifikansnivån och antalet frihetsgrader. Antalet frihetsgrader är, (r-1)*(c-1), där "r" står för antalet rader och "c" står för antalet kolumner. I vårt exempel enligt punkt 3 är det 3 rader och 2 kolumner vilket ger 2 frihetsgrader ((3-1)*(2-1)). X^2-värdet hämtas från en tabell över Chi-2 fördelning.

Beslutsregel, 5% signifikans, 2 frihetsgrader, höger-svans
Förkasta nollhypotesen och acceptera alternativhypotesen om X^2-värdet är större än 5,991. Förkasta inte nollhypotesen om X^2-värdet lika med eller mindre än 5,991.

5. Ta ett beslut
Det sista steget inom hypotestestning innebär att man skall ta ett beslut huruvida nollhypotesen skall förkastas eller ej. Vi har beräknat testestimatet (X^2) till 17,5 enligt punkt 3 ovan, detta värde är högre än det kritiska värdet om 5,991. Vi förkastar därför nollhypotesen och accepterar alternativhypotesen om att det finns ett samband mellan gymnasiebetyg och universitetsbetyg. Vi har kommit fram till att det finns ett signifikant samband mellan gymnasiebetyg och universitetsbetyg på signifikansnivån 5%.

Behöver ditt företag låna pengar? Hos Krea kan du jämföra olika företagslån helt kostnadsfritt. Klicka här och gör en ansökan redan idag, det är gratis och inte bindande. Du får låneförslag inom 48 timmar.

Vill du sänka dina levnadsomkostnader? Hos Zmarta kan du spara pengar på privatlån, bilförsäkring, hemförsäkring, elavtal, bolån och företagslån med mera. Klicka här och bankpressa dina lån idag, du kanske även hittar något annat att spara pengar på.

Låna upp till 500 000 kr utan säkerhet! Komplett Bank erbjuder ett flexibelt lån med en nominell ränta mellan 4,9 och 19,9 %, klicka här för att ansöka idag. Du kan betala av på lånet när du tycker att din ekonomi tillåter det och du får använda pengarna till vad du vill.