Regressionsanalys är en metod för att skapa en ekvation som
beskriver sambandet mellan två variabler, den oberoende och den
beroende variabeln. Regressionsanalys innebär också att uppskatta
värdet för den beroende variabeln genom att välja ett värde för den
oberoende variabeln. Inom regressionsanalys skapas en
regressionsekvation som beskriver sambandet mellan två variabler. En
regressionsekvation kan ritas upp som en linje i ett diagram.
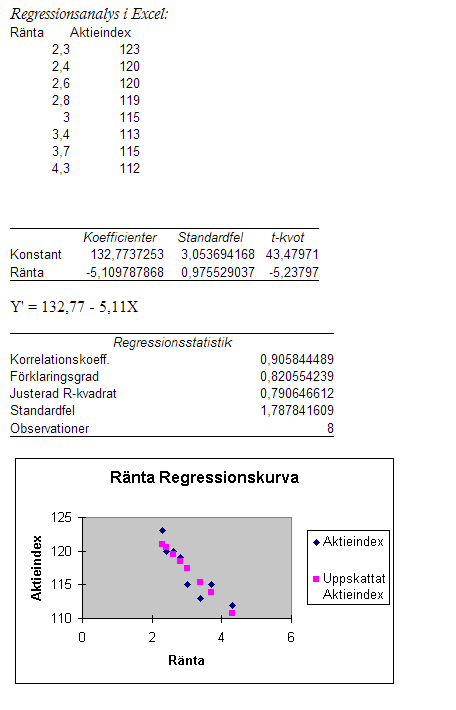
Regressionsekvationen:
Y' = a + bX
där:
Y' = Det prognostiserade värdet för Y för ett valt värde på X
a = Det uppskattade värdet för Y när X=0, är alltså det uppskattade
värde för Y där regressionslinjen korsar y-axeln när x är noll.
b = Är lutningen på regressionslinjen eller den genomsnittliga
förändringen för Y när X ändras med en enhet.
X = Är ett värde för den oberoende variabeln X, kan vara vilket
värde som helst.
Regressionslinjens lutning (b):
b = (n*(∑XY)-(∑X)*(∑Y))/(n*(∑X^2)-(∑X)^2)
Regressionslinjens skärningspunkt (a):
a = (∑Y/n)-(b*(∑X/n))
där:
X = Värdet för den oberoende variabeln
Y = Värdet för den beroende variabeln
n = Storleken på urvalet
(∑X^2) = X i kvadrat innan summering
(∑X)^2 = X variabeln summerad och sedan kvadrerad
(∑XY) = X multiplicerat med Y, produkterna summeras
Behöver ditt företag låna pengar? Hos Krea kan du jämföra olika företagslån helt kostnadsfritt.
Klicka här och gör en ansökan redan idag, det är gratis och
inte bindande. Du får låneförslag inom 48 timmar.
Vill du sänka dina levnadsomkostnader? Hos Zmarta kan du spara pengar på privatlån, bilförsäkring,
hemförsäkring, elavtal, bolån och företagslån med mera.
Klicka här och bankpressa dina lån idag, du kanske även hittar något annat att spara pengar på.
Låna upp till 500 000 kr utan säkerhet! Komplett Bank erbjuder ett flexibelt lån med en nominell ränta mellan 4,9 och 19,9 %,
klicka här för att ansöka idag.
Du kan betala av på lånet när du tycker att din ekonomi tillåter det och du får använda pengarna till vad du vill.